Practical Quad Mesh Simplification

Just a shameless plug to our last EG paper that will find is way inside MeshLab:

Marco Tarini, Nico Pietroni, Paolo Cignoni, Daniele Panozzo, Enrico Puppo
Practical Quad Mesh Simplification
Computer Graphics Forum, Volume 29, Number 2, EuroGraphics 2010

In our community it is well know the old religious war between quad vs. triangle meshes, each approach has its own merits and I not discuss them here.
Moving back and forth between the two approaches is often useful but the issue of getting a good quad mesh from a highly irregular tri mesh is a tough one.

In the above paper we present a novel approach to the problem of quad mesh simplification, striving to use practical local operations, while maintaining the same goal to maximize tessellation quality. We aim to progressively generate a mesh made of convex, right-angled, flat, equally sided quads, with a uniform distribution of vertices (or, depending on the application, a controlled/adaptive sample density) having regular valency wherever appropriate.

In simple words we start from a tri mesh, we convert into a dense quad mesh using a new Triangle-to-Quad conversion algorithm and then we simplify it using a new progressive quad simplification algorithm. The nice side is that the quad simplification algorithm actually improves the quality of the quad mesh. Below a small example.

We are currently adding this stuff inside MeshLab. The first things that will appear are the triangle to quad conversion algorithms and some functions for measuring the quality of a quad mesh according to some metrics. More info in the next posts....


(2/1/10 edit: if the above link for the paper does not work try this:  Practical Quad Mesh Simplification)

MeshLab on YouTube

Just a short post of a video created by Nicolò dell'Unto (a PhD student at IMT)
about the use of MeshLab and Arc3D for building up a 3D model of an archeological excavation and showing it inside a cave.



Side note, the data was collected during a workshop of the 3DCOFORM training series on “3D acquisition and post-processing” that took place at The Cyprus Institute in Nicosia on 2-6 November 2009 and that, among other things focused on the use of MeshLab for Cultural Heritage related activities.

3D scanning and unrolling an ancient seal

A few lines on an interesting recent project I participated and that exploited MeshLab processing abilities.
The project whose results are now shown in a exhibition at the Louvre involved the scanning with non traditional technologies of the very small and wonderful ancient Cylinder Seal of Ibni-Sharrum (photo © CRMF / D. Pitzalis), a precious antique mesopotamic artifact that is considered one of the absolute masterpieces of glyptic art.

This small seal was digitally acquired at CRMF at a very high resolution and with a variety of 3D scanning techniques (microprofilometry, x-ray Tomography, photogrammetric techniques) and, obviously, the results were processed and integrated entirely with MeshLab.

Among the nice things that we did inside MeshLab was the virtual unrolling of the seal, e.g. getting the inverse shape that you get when you roll the seal over a soft substance like clay or wax.  It was quite easy from a technical point of view, but very appreciated by the restorers that disregard invasive plaster based techniques that often can leave small residuals over the precious artifacts.  You can find more details on the whole acquisition and processing of the seal on this VAST conference paper.

 

On the side you can see a couple of renderings of the 2-million of triangle model of the unrolled seal; the renderings were done inside MeshLab, the first one is a simple flat shaded rendering, while the second one exploit a nice shader that I have recently added to the MeshLab shading arsenal, it mimics in a shameless way the ZBrush technique of varying shininess and color according to the "cavities" of the geometric model (they use it for the famous zbrush wax and bronze materials).  It is nice to see how the shading vastly improve the shape perception of the 3D model.
I have not seen many correct discussion on how to perform these kind of shading, so expects a post on that...


A massive physical reproduction (4 meters long!) of the unrolled seal is at the center of "OnLab" a thematic exhibition of Michel Paysant, that will open in the next days at Louvre, Denis Pitzalis worked a lot on this project and you can find  more details and photos in his blog.

MeshLab V1.2.2 Released!

Yet another minor release of MeshLab. This time a lot of large internal changes (we redesigned the parameter mechanism of the filters for a better previewing mechanism) and we added a few new features:
* pdb molecular importing to build up meshes from molecular description. It feature various ways of building meshes from pdb description.
* Weighted simplification; you can now weight the simplification process with a generic scalar value (e.g. simplify more the internal regions, preserve better the face of a character, etc, etc.).
* Improved the vertex attribute transfer filter (the filter that allows you to transfer color, vertex, position, quality from a mesh to another one) to support the management
of point cloud data and to limit the attribute transfer to a limited
distance.
* The new abstract surface parametrization algorithm in now inside MeshLab; currently it is a bit slow and buggy (well it is the first release) so sometime it can crash. The current version of the filter support only the remeshing side of the technique, e.g. you can create an abstract texture and then use it to remesh your model in a very nice way. Full texture parametrization of meshes ahead in the next version.
* And obviously a lot of small bug issues....
As usual release notes are here in the wiki.

Meshing Point Clouds

One of the most requested tasks when managing 3D scanning data is the conversion of point clouds into more practical triangular meshes. Here is a step-by-step guide for transforming a raw point cloud into a colored mesh.

Let's start from a colored point cloud (typical output of many 3D scanning devices), each point has just color and no normal information. The example dataset that we will use is a medium sized dataset of 9 millions of points. Typical issues of such a dataset dataset: it is non uniform (comes from an integration of different datasets), has some strongly biased error (alignment error, some problem during data integration), it comes without normals (hard to be shaded).

1. Subsampling
   
   
   
   As a first step we reduce a bit the dataset in order to have amore manageable dataset. Many different options here. Having a nicely spaced subsampling is a good way to make some computation in a faster way. The Sampling->Poisson Disk Sampling filter is a good option. While it was designed to create Poisson disk samples over a mesh, it is able to also compute Poisson disk subsampling of a given point cloud (remember to check the 'subsampling' boolean flag). For the curious ones, it uses an algorithm very similar to the dart throwing paper presented at EGSR2009 (except that we have released code for such an algorith long before the publication of this article :) ). In the invisible side figure a Poisson disk subsampling of just 66k vertices.
2. Normal Reconstruction
   
   
   
   Currently inside MeshLab the construction of normals for a point cloud is not particularly optimized (I would not apply it over 9M point cloud) so starting from smaller mesh can give better, faster results. You can use this small point cloud to issue a fast surface reconstruction (using Remeshing->Poisson surface reconstruction) and then transfer the normals of this small rough surface to the original point cloud. Obviously in this way the full point cloud will have a normal field that is by far smoother than necessary, but this is not an issue for most surface reconstruction algorithms (but it is an issue if you want to use these normals for shading!).
3. Surface reconstruction
   
   
   
   Once rough normals are available Poisson surface reconstruction is a good choice. Using the original point cloud with the computed normals we build a surface at the highest resolution (recursion level 11). Roughly clean it removing large faces filter, and eventually simplify it a bit (remove 30% of the faces) using classical Remeshing->Quadric edge collapse simplification filter (many implicit surface filters rely on marching cube like algorithms and leave useless tiny triangles).
4. Recovering original color
   
   
   
   Here we have two options, recovering color as a texture or recovering color as per-vertex color. Here we go for the latter, leaving the former to a next post where we will go in more details on the new automatic parametrization stuff that we are adding in MeshLab. Obviously if you store color onto vertexes you need to have a very dense mesh, more or less of the same magnitudo of the original point cloud, so probably refining large faces a bit could be useful. After refining the mesh you simply transfer the color attribute from the original point cloud to the reconstructed surface using the vertex attribute transfer filter.
   
   
5. Cleaning up and assessing
   
   
   
   The vertex attribute transfer filter uses a simple closest point heuristic to match the points between the two meshes. As a side product it can store (in the all-purpose per-vertex scalar quality) the distance of the matching points. Now just selecting the faces having vertices whose distance is larger than a given threshold we can easily remove the redundant faces created by the Poisson Surface Reconstruction.

This pipeline is only one of the many possible way of ending up into a nice mesh. For example different choices could have been done for step 2/3. There are reconstruction algorithms that do not need surface normals, like for example the "Voronoi Filtering" that is an interpolating reconstruction algorithm (e.g. it build up only triangles on the given input points) but usually these filters works better on very clean datasets, without noise or alignment errors. Otherwise on noisy datasets it is easy that they create a lot of non manifold situations. Final thanks to Denis Pitzalis for providing me this nice dataset of a Cypriot theater.

Computation & Cultural Heritage Siggraph Course

Shameless linking of the Computation & Cultural Heritage Siggraph Course where, a week ago, I gave my contribution. The course surveyed several practical CG techniques for applications in cultural heritage, archeology, and art history. Topics include: efficient/advanced/cheap techniques for 2D/3D digital capture of heritage objects, appropriate uses in the heritage field, an end-to-end pipeline for processing archeological reconstructions (with special attention to incorporating archeological data and review throughout the process), how digital techniques are actually used in cultural heritage projects, and an honest evaluation of progress and challenges in this field.

Specifically to this blog in my first presentation I described a free photo to 3D pipeline that relies on the free web-based service Arc3D (developed during the Epoch EU project by Visic of KUL) for Structure-from-Motion reconstruction and (obviously) on MeshLab for the processing of the generated 3D range maps. In practice it is a pipeline that allows to cheaply reconstruct nice accurate 3D models from just a set of high resolution photos. Obviously not all the subject fit with this kind of approaches (forget moving subjects and glassy, shiny, fluffy, iridescent stuff), but for stable, dull, textured objects, it works surprisingly well, giving results with a quality not far from traditional laser based 3D scanning. More info on the process in the slides (and eventually in other posts here). In the top right picture a typical example of the results that you can obtain when starting from a reasonable set of photos of a detail of a weathered stone romanesque high relief (Monasterio de Santa María de Ripoll). The model is untextured, with just a bit of ambient occlusion: all you see is geometry.

Almost isometric mesh parameterization

A short post after a long inactivity just before going to Siggraph.


Many users of MeshLab complained the lack of texturing tools. As you probably know perfect, nice, clean, robust, automatic texture parametrization is a kind of 'holy grail' in CG. There are many many solutions around and a huge literature on that, but no silver bullet.
We (mostly Nico and Marco) added our 5 cents to the literature with yet another approach [1] that is able to produce parametrizations that exhibit a very low distortion and are composed by a small number of large regular patches. The parametrization domain is a collection of equilateral triangular 2D regions enriched with explicit adjacency relationships (we call it abstract because no explicit 3D embedding is necessary). It is tailored in order to minimize the distortion, resulting in excellent parametrization qualities, even when meshes with complex shapes and topology are mapped into domains composed of a small number of large contiguous regions.

An interesting consequence of having a texturing domain that is composed by 'abstract' equilateral triangles is that you can exploit this parametrization to build high quality remeshing that are better that the current state of the art. Look at the top figures to get an idea of the quality of the produced meshes. As usual all the gory details of the technique in the below paper preprint and a working open source implementation in the next versions of MeshLab.




[1] Nico Pietroni, Marco Tarini, Paolo Cignoni, Almost isometric mesh parameterization through abstract domains, IEEE Transaction on Visualization and Computer Graphics, Volume In press - 2009

MeshLab V1.2.1 Released!

Initially this release was planned just as a bug fixing release (a really needed one!): a couple of really annoying bugs infiltrated the 1.2.0 release, causing crashes for all the tools that involved a marching cube processing and malfunctioning of the U3D exporting. Now they should work well.

In practice it is a feature rich release: as a bonus we have added some new nice functionalities (thanks to M. Sottile for implementing them): Convex Hull, Alpha shape, Voronoi Filtering, and Visible points filters. These filters rely on the well known Qhull convex hull library.
Convex hulls and Alpha shapes do not need extensive introduction, but a few notes on the two other filters are probably needed.

Voronoi filtering implements the homonym surface reconstruction algorithm by Nina Amenta and Marshall Bern that is able to reconstruct a nice interpolating triangulated mesh from a point clouds. It requires nicely sampled, low noise point clouds, but it works well.

The Visible Points filter implements a nice algorithm of Sagi Katz, Ayellet Talfor and Ronen Basri for computing direct visibility of point clouds. It is a really really simple and smart trick that works well and it is really easy to be implemented (once you have a convex hull implementation).

As usual, release notes are here in the wiki.

MeshLab V1.2.0 Released!

After more than one year from version 1.1.1, the long, long waited MeshLab v.1.2.0 has
been released! Jump over the main page and download it.

http://www.meshlab.org

A sincere thank-you to every contributor and, in particular, to Guido Ranzuglia
that has willingly taken the demanding and onerous task of coordinating
(e.g. actually performing) the whole release process.
Next release cycles, in particular for bug fixing releases, will be much
shorter...
With respect to v1.1.1 the list of new features is very very long, now more than 100 different filtering actions are provided. In the next post I will spot some of the most interseting algorithm that have been added. In the meantime just download and try it!

MeshLab at Archeo-Foss (2)

Yet another non technical post :)
I have just returned from the Rome ArcheoFoss workshop. Being one of the organizers I can be proud of the success of the event, more than 150 people from the archeological field attended to the event crowding the main room of the CNR central building. I did not think that such a strictly focused event could attract such a wide audience; it seems that the intersection of people that have a genuine interest in Archeology, believe in open solutions, and live in Italy is a significant set :).
We (Guido Ranzuglia was the speaker) kept a short (40 min) tutorial on MeshLab, to a very interested, non computer scientist, audience; hopefully in a short time there should be a video available.
Pleasant discoveries: MeshLab is already well known in the field as a low cost alternative of the well known big names in 3D scanning processing tools. I also discovered that MeshLab was included in a ArcheoOS a linux distribution targeted to Archeological people.

MeshLab at Archeo-Foss

Just a short news about one of the many public presentation of MeshLab.
This time we will talk about MeshLab at the Archeo-Foss Workshop, the fourth Italian workshop on Free software, Open source and Open formats in the archaeological field. The workshop will be held in Rome on April 27-28, and it will be centered on the importance of open source sw and process in archaeology, not only considering the price issues, but also taking into account, long term sustainability and process documentation issues.

As you can imagine in this field MeshLab well cover the role of the open source alternative of the various high priced systems for 3D scanning data processing (most of them are priced in the 10k~30k $ range). In the Cultural Heritage environment budget resources are ofter very scarce and cost issues are seriously considered. Here source solutions play a very important role.

We often collaborate with many different CH institutions, working on wonderful ancient masterpieces. Something that often fully repay the effort done in the processing...

Below a few of the Lunigiana statue menhir that we recently acquired and processed (precisely he did most of the job, thanks Marco!).

How to remove internal faces with MeshLab

A very common situation that often arise the cleaning of a model with a detailed interior in which you are not interested in (and you want to remove it once for ever!). For example consider this nice LEGO model: 200k faces. Most of the faces are hidden inside the model, used to describe the internal pieces and pegs: not very useful in most cases. We can remove them with MeshLab.

After starting the filter color->vertex ambient occlusion over the mesh (and after waiting a few seconds) we have computed both a per-vertex gray color and stored for each vertex an attribute with a occlusion value. Side note: MeshLab has a general purpose per vertex and per face scalar quantity that are used and interchanged by many different algorithms with a variety of different semantic; we call this scalar quantity "quality" for no good reason (lazyness), it is a generic scalar quantity, it could be occlusion value (like in this case), a geodesic distance from border, gaussian curvature.

Second note: Ambient occlusion greatly enhance the perception of 3D shapes! Nowadays everyone recognizes it, but a few years ago not a lot of people was really aware of that (I am a proud user of AO since 2001 for nice renderings of Cultural Heritage stuff :) and, more recently, for nice renderings of molecules ).

Back to the topic of removal of internal faces.

We now can exploit this per-vertex occlusion value to select all the faces that have all their three vertices with a very low occlusion value. That means that we remove all the faces that has no visible vertices. This is not an perfect solution, there are easy counter-examples where this approach could remove visible faces (but with hidden vertices): in most cases it works wells but a bit of caution is always recommended.
In the side figure you can see the select by vertex quality filter in action with the all the selected internal faces: 130k faces out of 200k were totally internal and can be safely removed leaving just 70k faces.

On the computation of vertex normals

Computing per-vertex normal is usually a rather neglected task. There is a very popular solution that is usually considered reasonable and good for all purposes, until you hit some nasty counter-examples... Short summary of the most common approaches:

1. Compute an area weighted average of the normals of all the faces incident on the vertex. This is the classical approach, very handy, just because if you compute your face normals using a simple cross product between two edges of a triangle, you get for free a normal vector whose length is twice the triangle area. So just summing the un-normalized cross products gives you the right weights. Referred many many times as THE method for computing per vertex normals.
   
2. Compute an angle weighted average of the normals of all the faces incident on the vertex. Probably first seen on [1]. Mathematically sound, in the sense that it catch the limit behavior of the surface in a local neighborhood of the vertex. Simple, but it requires some trigonometric computations, so it is usually neglected by hard core optimization fans.
3. Use the "Mean Weighted by Sine and Edge Length Reciprocal" proposed by N. Max [2]. One of the many possible variations of smart weighting with the nice property of NOT using trigonometric computations.
   

Without going into gory details (that you can find in [3]), you should know that the classical approach can give rise to some VERY counter-intuitive normals. Below a practical example of the difference between the above three algorithms. Note how the direction of the normals on the top of the thin up-wedges is strongly biased by the underlying tessellation. Yes this is a rather badly triangulated nasty example, but this stuff happens.

Just for fun (and to overcome a bug in another algorithm) we have added the three explicit methods for computing normals in the latest beta of MeshLab. Personal, un-scientific, subjective feelings:

1. simple but dangerous
2. good
3. almost good
   

[1] G. Thurmer, C. A. Wuthrich, "Computing vertex normals from polygonal facets"
Journal of Graphics Tools, 3 1998
[2] Nelson Max, "Weights for Computing Vertex Normals from Facet Normals", Journal of Graphics Tools, 4(2) (1999)
[3] S. Jin, R.R. Lewis, D. West, "A comparison of algorithms for vertex normal computations", The Visual Computer, 2005 - Springer

Creating Voronoi Sphere (2)

Second part of the description of how this voronoi sphere was created.

At the end of the previous post we ended with a thin surface representing a sphere holed with a voronoi pattern.

1. convert the paper-thin surface to a solid structure.
   This can be done by exploiting the offsetting capabilities of MeshLab. The filter "Remeshing->Uniform Mesh Resampling". In this filter a mesh is re-sampled by building a uniform distance-field volumetric representation where each voxel contains the signed distance from the original surface. The surface is then reconstructed using the marching cube algorithm over this volume. Resolution of the volume obviously affects the resolution (and the processing time!) of the final mesh. The distance field representation allows to easily create offset surfaces. There are various options for building offset surfaces, I will discuss them deeply in another post, for now just set the "Precision" parameter to 1.0%, and the offset value to 53.0% and check the "Absolute Distance" flag. After a few tens of secs you should get something like the side figure.
   
   
   


2. simplify a bit to get rid of the bad triangulation quality of a Marching Cube (there are a lot of thin bad shaped triangles around), a percentage reduction of .75 is usually enough to both reduce a bit the size of the mesh and to improve its quality without affecting in a significant way the precision of the result.
   
   
   
   
   
   
   
3. Apply a few times the Filter Remeshing->Curvature flipping optimization, that improves how the triangles adapt to the shape of the curvature without increasing their number.
   
   
   
   
   
   
   
   
   


4. Refine and smooth up to a mesh of approx 1.000.000 triangles.
   A rather overtessellated mesh is needed here to guarantee a good approximation of the geodesic distance.
   
   
   
   
   


5. At this point we repeat no this dense mesh the same steps we did on the original sphere. E.g. all the steps described in the previous post:


1. Generate 1000 poisson samples over the surface (it takes a bit of time this time...)
   
   
   
   
2. Color the mesh according to the back distance from these samples (voronoi coloring filter)
   
   
   
   
3. select the faces with quality in the range 0..epsilon
   
   
   
   
   
4. invert selection and delete
   
   
   
   
   
5. offset the thin surface to convert it into a watertight solid object. This final offsetting obviously require an higher precision (and higher processing times).
   
   
   
   
6. Some iteration of simplify-optimize-refine-smooth just to beautify the final mesh.
   

And that's all! Varying a bit the parameters in the middle of the whole process greatly affect the final result. For example you can easily get a fat donut style by increasing the offsetting value. Below a high res snap done with meshlab with ambient occlusion, and thin antialiased wire frame lines. A real, touchable 3D print of the object can be obtained on Shapeways.

On the storage of Color in meshes

A very short post to clarify a bit the ways in which people can store color (and other) information on a mesh. AFAIK there are mostly three ways to keep color:

• Per-vertex: each vertex stores a color. A triangular face can have vertexes of different color and inside a triangle the color is linearly interpolated. Color is smooth across the surface.
  
• Per face: each face has a distinct color. You can easily see the discontinuity of colors among the faces (no interpolation is usually done.
• As texture: the most general way that is reasonably decoupled from the mesh itself. You only need a good parametrization.

In MeshLab most of the algorithms (painting, color processing etc.) manage per-vertex color, but a few conversion tools are provided.

• per-vert -> per -face
  
• per-face -> per-vert
• texture -> per-vert

A per-vert -> texture is strikingly missing :). To be added in the very near future. Obviously assuming the previous existence of a parametrization...
A fourth technique could be mentioned, keeping stuff per wedge, i.e. for each corner of the face we can store different colors (or other attributes), but this approach is rather unused (it can be simulated by duplicating vertices).
Below a few images showing the difference between the three modes on a small (40k tri) mesh; respectively: no color (to give you an idea of mesh density), color by texture, per vertex color, per face color.

Creating Voronoi Sphere

February 2016 update. You can make it online without even installing anything, by using the new browser based version of MeshLab: www.meshlabjs.net 

MeshLab is quite useful for a lot of classical mesh processing tasks, but sometimes it can be used for more weird things. A few weeks ago, after stumbling upon the cool Shapeways 3D printing service I uploaded there a few artsy mathematical sculptures that I created with MeshLab. Here is how I did this one, called Voronoi sphere.
It is a double Voronoi diagram, in the sense that there is a coarse Voronoi diagram over the sphere surface but also the surface that creates the edges of this diagram has been carved to create another finer Voronoi diagram. Such a shape is really very light and thin but much more robust that you could imagine.

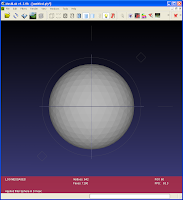
1. Start from a sphere (file->new->Sphere),
   
   
   
   
   
2. Refine it using Filter>Remeshing>Loop Subdivision surfaces. repeat without shame (lowering the edge threshold parameter) until it becomes reasonably well tessellated. 300k faces are enough.
   
   
   
   
3. Create some well distributed samples over the surface using
   Filter>Sampling>Poisson Disk Sampling. 50 points are a good choice. Apparently the filters does nothing, but if you reveal the layer panel (guess the icon in the toolbar :)), you can see that there are two layers. Make invisible the first layer and switch the rendering mode to points: you will see the well distributed Poisson samples (hint: alt+mouse wheel change the drawn size of the points).
   
   
4. Create the actual Voronoi diagram by simply choosing the filter
   Color>Voronoi Vertex Coloring. As reported in the top of the parameter window, this filter, given a mesh M and a point-set P, project the points of P over M and color each vertex of M according to the geodesic distance from these projected points. Marking the backdistance flag in the parameter window the filter computes the distance from the borders of the Voronoi diagram instead of the projected sites itself. This filter, beside coloring the mesh, writes on each vertex of the mesh the distance value itself, in the all-purpose attribute named 'quality'.
   
   
   
5. Make the mesh layer active, and start the Select by vertex Quality filter. enable the preview option and enable visualization of selected faces. Play with the slider until you get something similar to the image on the right; in practice, exploiting the quality value stored onto the vertices that code the distance from the border of the Voronoi diagram we have just selected the faces very near to these borders.
   
   
   
   
   
6. Apply the Filter>Selection>Invert Selection and then delete the selected faces. Edges are probably quite jaggy, so apply a couple of times the simplest of all the smoothing filter, the old classical laplacian filter (Filter>Smoothing>Laplacian Smoothing).

Now stop and save the mesh. Next post will show you how to continue by transforming the current mesh, that is a surface, into a solid object ready to be printed. In the meantime if you like the sculpture, you can buy a small (10 cm) and cheap (less than 20$) copy of this sculpture here.

Creating Interactive 3D objects inside a PDF

One of the nice feature of MeshLab is its ability of saving meshes, in a variety of formats. Support for saving meshes in U3D format is useful for creating, using LaTeX, cool appealing PDFs with embedded 3D models.

Yes, that means that when, using a plain Acrobat Reader, you open a pdf like this one, you will be able to freely interact with the 3D model, directly inside the text.

To generate such a pdf you simply need to convert your mesh into u3d format, and include the small snip of latex code generated by MeshLab with the right viewing parameters, in your latex document and simply compile it with pdflatex. Thanks to the Movie15 latex package, you will have your u3D embedded in the pdf. Note that the u3d file format is quite compact; for an example you can look at this pdf that contains the 50k triangle mesh of the Laurana's bust squeezed to less than 250 kb. A zip with sources (latex and u3d file) can be found here.

A couple of notes. The conversion process is done through the use of the Universal 3D Sample Software by directly using the IDTF converter provided with the sample library. The conversion process can take a fairly long processing time (many seconds for a mesh composed by 50k triangles) so be patient! Moreover be careful that the process can fail when involving pathnames with non trivial chars. Moreover very large meshes take a LONG time to be converted, be patient... Acrobat reader support this kind of files since ver. 7.

On the subtle art of mesh cleaning

Most mesh processing algorithms usually require nice two-manifold, watertight, intersection free, well-shaped, clean meshes. Obviously in the real world this does not happen with a great frequency (apart in scientific papers). Common meshes are the most horrible mix of all the possible almost catastrophic degenerate situations.

MeshLab can help the tedious tasks of cleaning meshes in a variety of ways. Let's start with some simple examples involving vertices.

1. Unreferenced Vertices. Very common issue. Your mesh has some vertices that are not referenced by any triangle. A variety of cause can create these situations (algorithms deleting faces in a non careful way can create them). This situation can be more dangerous than it seems, because they can bring in trash uninitialized data in algorithms that initialize vertex data performing face-based traversal (e.g. normals computations...).
   An easy way to look at the presence of these vertices is simply switching to a point based rendering mode (evenually turning the lighting off, because, by default, unreferenced vertices have null normals). As always happens, sometime this situation is not an error but could be a feature (think to point clouds).
2. Duplicated vertices. Adjacent triangles does not share the vertices with the same coordinates. Sometimes it is an issue that come directly from some file formats (STL for example store triangles duplicating each vertex). This situation is easy to be detected:
   
   1. Smooth shading is the same of flat shading: the duplicated vertices do not allow the averagin of normals between adjacent faces that is necessary for smooth shading.
      
   2. Poor man version of Euler Characteristic does not work: instead of having:
      
      [face number] ~ 2 * [vertex number]
      
      you have:
      
      [face number] ~ 1/3 * [vertex number]
      
   Again this could be a feature and not an error. Sometimes, duplicating vertices can be used to impose sharp angles when you do not have simple techniques to store multiple normals for the same vertex.
   

The above cases can be cured, if necessary, by invoking in MeshLab the two filters, Remove Unreferenced Vertices and Remove Duplicated Vertices in the menu named: Filters->Cleaning and Repairing.

First Post

A bit of introduction on the purpose of this blog.
The most common comment that I receive from people that see MeshLab in use is "wow, I did'nt know it could be done..."
The main idea is to report here examples of trivial and less trivial uses of MeshLab in real, on the field (more or less), practical, applications.

A first note. All the posts will refer to stuff done with the latest available betas, e.g. the ones that you can download from the Wiki of MeshLab:
Beta Version of MeshLab